2011. INFORMATIONS ET PROGRAMMES
INFORMATIONS
Responsables du stage: Thierry Champion (mail) et Jean-Pierre Zanotti (mail).
Le stage concerne 16 participants de classe de seconde des lycées du Coudon,
de Dumont d'Urville et de Rouvière. Le stage se déroule sur deux journées, les jeudi 16 et vendredi 17 juin, dans les locaux de l'UFR-Sciences et Techniques de l'Université du Sud-Toulon-Var (salles T').
Deux groupes de 8 lycéens suivront 4 ateliers répartis sur 4 demi-journées (9h-12h puis 14h-17h). Les thèmes de ces ateliers sont:
- Jeux et invariants mathématiques;
- Raisonnement mathématique, du concret à l'abstrait;
- Autour des longueurs, surfaces et volumes;
- Représentation des fonctions numériques.
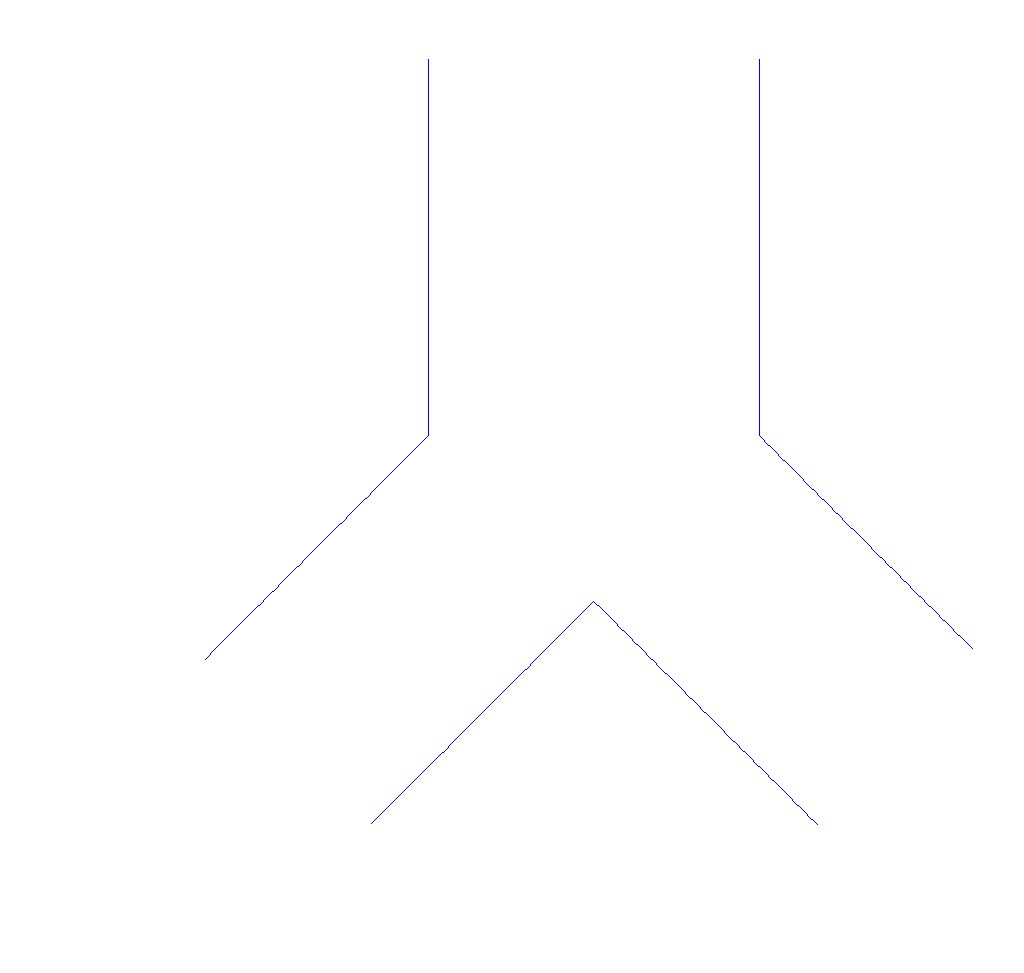
L'accueil se fera le jeudi matin entre 8h30 et 8h45 devant l'entrée du bâtiment V (cf. plan ci-dessous). Les déjeuners servis au CROUS de l’université sont pris en charge par l’organisation.
SOUTIEN FINANCIER
La manifestation a été financée avec la participation de
LES ATELIERS
Jeux et invariants mathématiques.
Thierry Champion.
Dans cet atelier, nous aborderons quelques jeux dont l'étude fait intervenir un invariant :
l'objectif est de montrer que la recherche d'invariants, qui est à la base de nombreux raisonnements mathématiques (en géométrie, mais aussi en arithmétique avec par exemple la preuve par neuf),
est un outil puissant dans l'étude de ces jeux.
Nous traiterons les jeux suivants :
Pavage en dominos
On considère un quadrillage
carré 4x4 de 16 cases, dont on retire deux coins (soit en diagonale, soit sur un même côté).
On se demande s'il est possible de
paver ce quadrillage "à moitié écorné" avec des dominos
qui ont tous une dimension de 2 cases. On généralisera ensuite cette question à des situations plus compliquées,
où le pavage est plus grand, ou rectangulaire, ou à trous.
Le turlupin
Le défi est ici d'écrire le mot turlupin sur un quadrillage
carré 3x3 de 9 cases auquel on retire une case: "écrire le mot
TURLUPIN" signifie qu'on doit poser les lettres de façon à ce qu'on puisse lire le mot en passant d'une case à sa voisine sans aller en diagonale. Ensuite on se demandera si on peut écrire
TURLUPINADE sur une quadrillage 4 x 3 auquel on retire une case.
Le solitaire
Des pions sont disposées sur un plateau de jeu. Le but du jeu est d'éliminer tous les pions du plateau sauf un, en appliquant le principe du "saute-mouton". Un pion peut sauter par dessus un autre et ainsi l'éliminer du plateau si ce dernier est situé sur la même ligne ou la même colonne et que la case d'arrivée est vide.
On peut trouver deux modèles de jeu de solitaire dans le commerce, on essaiera de déterminer si ces jeux admettent ou non une (des) solution(s).
| |
♙ | ♙ | ♙ |
| |
| |
♙ | ♙ | ♙ |
| |
| ♙ | ♙ |
♙ | ♙ | ♙ |
♙ | ♙ |
| ♙ | ♙ |
♙ | | ♙ |
♙ | ♙ |
| ♙ | ♙ |
♙ | ♙ | ♙ |
♙ | ♙ |
| |
♙ | ♙ | ♙ |
| |
| |
♙ | ♙ | ♙ |
| |
|
|
| |
♙ | ♙ | ♙ |
| |
| ♙ |
♙ | ♙ | ♙ |
♙ | |
| ♙ | ♙ |
♙ | ♙ | ♙ |
♙ | ♙ |
| ♙ | ♙ |
♙ | | ♙ |
♙ | ♙ |
| ♙ | ♙ |
♙ | ♙ | ♙ |
♙ | ♙ |
| ♙ |
♙ | ♙ | ♙ |
♙ | |
| |
♙ | ♙ | ♙ |
| |
|
Le taquin
Le taquin est constitué d'un plateau carré sur lequel coulissent horizontalement et verticalement 15 pièces numérotées de 1 à 15. La position initiale des 15 pièces est la suivante:
| 1 | 2 |
3 | 4 |
| 5 | 6 |
7 | 8 |
| 9 | 10 |
11 | 12 |
| 13 | 15 |
14 | |
Le problème consiste à placer correctement les pièces 14 et 15 si cela est possible.
Raisonnement mathématique, du concret à l'abstrait
Jean-Pierre Zanotti.
L'objectif de l'atelier est de mettre en évidence certains aspects fondamentaux du raisonnement en mathématiques et en particulier des mathématiques appliquées:
- la modélisation, ou comment l'on passe d'un problème concret énoncé en langue naturelle à un problème abstrait et l'importance du travail de simplification préalable.
- le codage, ou le formalisme utilisé pour cette modélisation et le choix de la théorie appropriée pour analyser et résoudre le problème.
- l'intuition, indispensable pour forger un raisonnement mais qui peut s'avérer être une source d'erreurs surprenantes.
Les problèmes susceptibles d'être abordés dans l'atelier:
Tournoi de tennis
Un tournoi de tennis comporte 1025 participants. L'élimination est directe. A chaque tour les rencontres sont tirées au hasard (s'il y a un nombre impair de joueurs en lice, celui qui ne joue pas le fera nécessairement le tour suivant). Combien de rencontres auront été disputées durant le tournoi pour déterminer le vainqueur ?
Les fléchettes
Une machine lance des fléchettes au hasard sur une cible circulaire inscrite dans un carré d'1m de côté. Certaines fléchettes tombent dans le cercle, d'autres à côté (donc entre le cercle et les angles du carré). Un compteur qu'on initialise à 0 affiche en permanence le nombre de fléchettes f qui ont atteint la cible. Après n tirs, on calcule le rapport f / n. Que va devenir ce rapport quand n devient très grand ?
L'architecte
Un architecte a dessiné les plans d'un bâtiment rectangulaire destiné aux mathématiciens toulonnais. Ils ont demandé à l'architecte à ce que le bâtiment respecte la condition suivante: si on lui retire le plus grand carré à l'une de ses extrémités (soit un carré de côté la largeur du bâtiment), le rectangle restant a exactement les mêmes proportions que le bâtiment entier. La condition fixée par les mathématicients est-elle réalisable ?
Les verres de vin
Un vigneron remplit deux verres identiques d'un même volume de vin, le premier verre avec du vin rouge, le second avec du vin blanc. Il prélève une quantité de vin du verre de vin rouge à l'aide d'une cuillère et la mélange dans le verre de vin blanc. Il prélève ensuite exactement la même quantité de ce mélange et la verse dans le verre de vin rouge. Y-a-t-il plus de vin rouge dans le verre de vin blanc que de vin blanc dans le verre de vin rouge ?

Les trois frères
La somme des âges de trois frères est 35 ans et le plus agé d'entre eux à 2 fois l'âge du plus jeune. Quel est l'âge de chacun des trois frères ?
L'escalade
Deux alpinistes se retrouvent sur un grand plateau face à une paroi verticale qu'ils doivent gravir. Ils se demandent s'ils auront assez de longueur de corde. L'un des alpinistes mesure 1,80m et l'autre chausse du 45 (la pointure d'une chaussure est égale à 1,5 fois la taille du pied en centimètres). Comment les deux alpinistes doivent-ils procéder pour faire une bonne estimation de la hauteur de la paroi ?
Le rendez-vous
Deux élèves doivent se retrouver entre 12h00 et 13h00 devant le bassin de la Place de la Liberté mais ni l'un ni l'autre n'est en mesure de connaître l'heure exacte à laquelle il pourra être sur place. Chacun promet à l'autre de l'attendre 10 minutes mais pas plus et ce jusqu'à 13h00 au plus tard. Quelle est la probabilité qu'ils se rencontrent à ce rendez-vous ?
L'escargot et la laitue
Un escargot est à une distance de 3m d'un mur haut de 2m et de 20cm d'épaisseur. De l'autre côté du mur, une délicieuse salade l'attend. Elle est située à 5m du mur et à 2 mètres de la droite correspondant à la direction de l'escargot. Quelle est la longueur du chemin le plus court que doit parcourir l'escargot pour manger la salade ?
On perd la boule
k boules régulièrement espacées roulent sur une piste dans la même direction. En face d'elles
n autres boules roulent en sens inverse. Quand deux boules se rencontrent, elles repartent chacune en sens inverse. En supposant que la piste est infinie de part et d'autre, qu'il n'y a pas de frottements, que les boules ont la même masse et la même vitesse, combien de collisions auront lieu ?
|
... | ⚫ |
→ | ⚫ |
→ | ⚫ |
→ | |
| |
← | ⚫ |
← | ⚫ |
← | ⚫ |
← | ⚫ |
... | |
Les concombres
Un concombre est constitué de 99% d'eau à la cueillette. Les consommateurs se méfiant du concombre, un stock de 500kg qui avait été entreposé à la coopérative juste après la récolte n'a pas trouvé d'acheteur après trois jours. A cause de la chaleur et l'évaporation, les concombres contiennent à présent 98% d'eau. Quel est le nouveau poids de ce stock de concombres ?
Le peloton
Pendant le tour de France, un peloton de cyclistes occupe une longueur de 100m sur la route et roule à vitesse constante. Le cycliste en tête du peloton et le cycliste en queue ont échangé leurs casquettes par erreur. Ils veulent les récupérer durant la course. Un motard leur vient en aide, il prend la casquette du dernier cycliste, l'emmène au cycliste en tête, fait l'échange et ramène sa casquette au dernier cycliste. Pendant toute l'opération, le peloton a parcouru 100m. Quelle est la distance parcourue par le motard pour la réaliser ? (Le motard roule en ligne droite et on néglige le demi-tour et la durée de l'échange).
La mouche et les TGV
Deux TGV roulent en direction l'un de l'autre sur la même voie, le premier à 320km/h, le second à 280km/h. Les deux TGV sont partis au même moment à 8h00, l'un de la ville de Brest, l'autre de Nice distantes de 1000 km. Un mouche dopée aux amphétamines s'envole au même moment du pare-brise du premier TGV et suit la voie pour arriver au pare-brise du second TGV, fait demi-tour et recommence cette partie de ping-pong. A quel moment la mouche sera écrasée entre les deux TGV ?
Autour des longueurs, surfaces et volumes
Didier Jesslé.
Le tour du monde
On ceinture la planète avec une corde au niveau de l'équateur. Quelle longueur de corde faudrait-il ajouter à cette ceinture si on l'écartait d'un mètre de la surface de la Terre sur toute la circonférence ? NB. Le rayon de la Terre est de 6400km environ.
Le rail
Un rail de chemin de fer d'un kilomètre de long est posé au mois de décembre. En été la température s'élève et le rail se dilate d'un mètre mais comme il est solidement arrimé à chacune de ses extrémités, il se soulève en son centre. Quelle hauteur va atteindre le point central (est-ce de l'ordre du centimètre, de la dizaine de centimètres, du mètre, de la dizaine de mètres) ?
Balade à New-York
La ville de New-York est quadrillée par des routes horizontales et verticales délimitant des blocs rectangulaires de 100m x 80m. On veut se déplacer d'un carrefour A à carrefour B. Il y a évidemment plusieurs chemins pour faire ce trajet. Est-il efficace de rapprocher son trajet de la ligne droite entreA et B ? Peut-on adopter une autre stratégie ?
Les pizzas
Donatello prépare 500g de pâte à pain pour cuisiner deux pizzas. Il dispose pour les cuire de deux plaques circulaires, l'une de 15cm de diamètre, l'autre de 30cm. Comment doit-il répartir les 500g de pâte ?
Le punch au citron
Dans la liste des ingrédients d'une recette de punch, il faut 5 citrons jaunes, mais le barman ne dispose que de citrons verts dont le diamètre est deux fois plus petit. Combien de citrons verts faut-il ?
La tuile
Dans le midi de la France les toitures doivent respecter une pente de 30%. Sur le plan d'une maison avec un toit à deux pans, la toiture occupe au sol un rectangle de 6 x 8m. Quelle surface de tuiles faut-il acheter ? Même question en montagne où la pente doit atteindre 60%.
On souhaite à présent couvrir un toit d'église en forme de cône avec de petites pièces en ardoise. Que se passerait-il si la pente devenait de plus en plus importante ?
Représentation des fonctions numériques
Cédric Galusinski.
A l'aide d'un logiciel gratuit de visualisation (Visit), la représentation de fonctions définies sur R x R (voire R x R x R)
à valeurs réelles sera introduite. La représentation locale de la
surface de la terre est l'application immédiate: l'altitude d'un lieu
en fonction de sa latitude et de sa longitude définit un point de la
surface de la Terre. On insistera sur la représentation de ces
fonctions par des surfaces en 3D ou des courbes de niveaux en 2D.
L'introduction de ces notions suit le plan suivant:
- Rappels sur les fonctions définies sur les réels et à valeurs réelles.
- Introductions des fonctions de R x R dans R:
- les fonctions radiales;
- la représentation dans R par des surfaces (altimétrie);
- la représentation dans R2 par des courbes de niveaux;
- représentation sur le logiciel Visit;
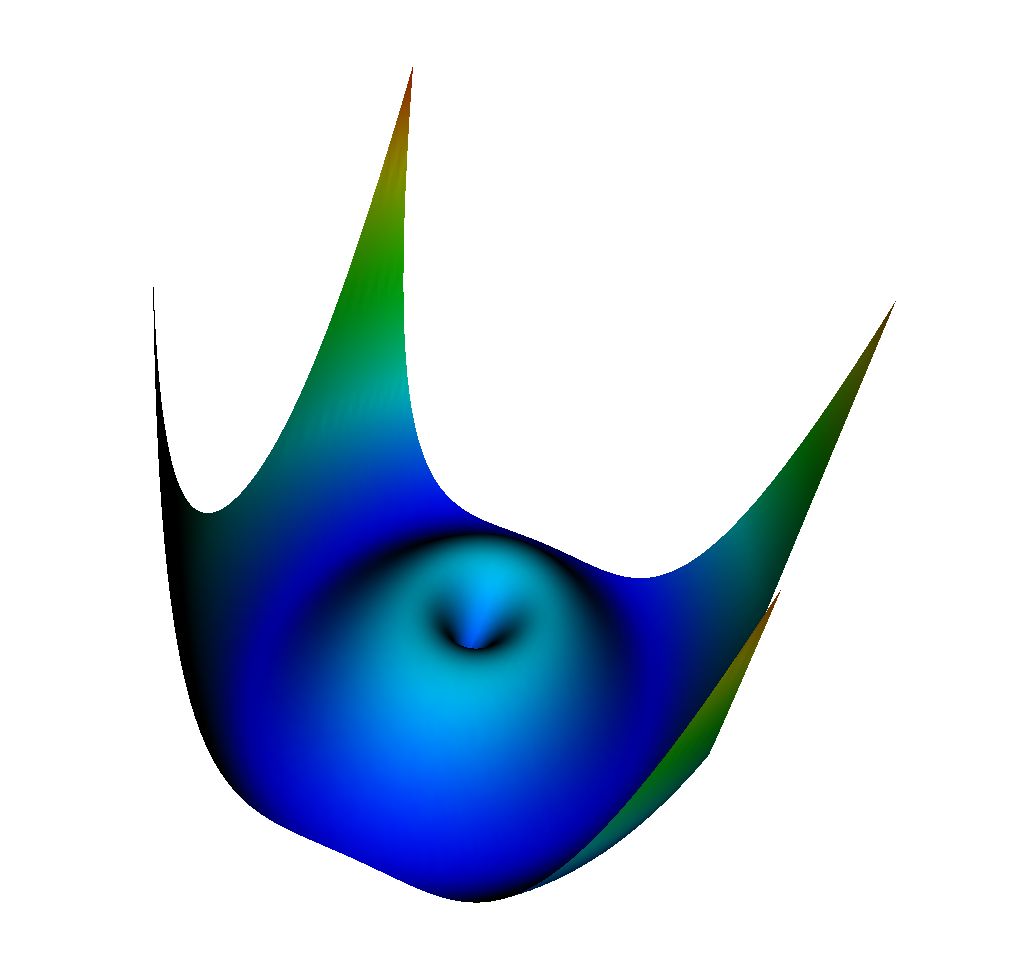
- visualisation d'une cartographie en relief;
- visualisation d'une cartographie par lignes de niveaux;
- construction d'exemples de fonctions sur Visit, exemple:
f(x, y) = ax2 + by2 selon a et b
- Introduction de la notion de col et point selle
f(x, y) = x2-y2, g(x,y) = xy.
- Exercices plus difficiles de construction de fonctions et visualisation
- une montagne en forme de lune: localisation de maximum en x à y fixé
- représentation d'un bord de fleuve par l'iso zéro de la profondeur d'eau
- inventer une fonction pour une portion droite de fleuve puis pour le delta du Rhone.
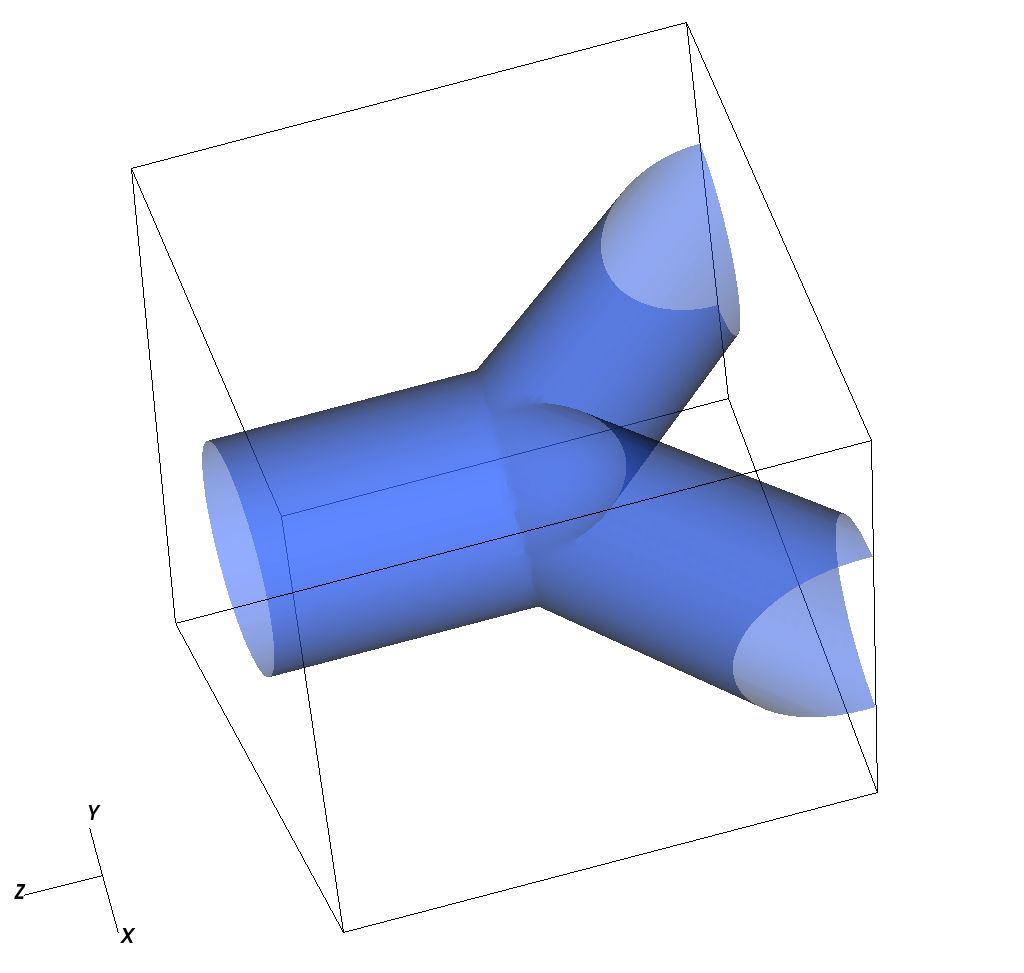
- généralisation 3D pour des constructions tubulaires.